Введение в системы управления базами данных
НФ (Четвертая Нормальная Форма)
4НФ (Четвертая Нормальная Форма)
Рассмотрим следующий пример. Пусть требуется учитывать данные об абитуриентах, поступающих в ВУЗ. При анализе предметной области были выделены следующие требования: Каждый абитуриент имеет право сдавать экзамены на несколько факультетов одновременно. Каждый факультет имеет свой список сдаваемых предметов. Один и тот же предмет может сдаваться на нескольких факультетах. Абитуриент обязан сдавать все предметы, указанные для факультета, на который он поступает, несмотря на то, что он, может быть, уже сдавал такие же предметы на другом факультете.
Предположим, что нам требуется хранить данные о том, какие предметы должен сдавать каждый абитуриент. Попытаемся хранить данные в одном отношении "Абитуриенты-Факультеты-Предметы":
НФ (Пятая Нормальная Форма)
5НФ (Пятая Нормальная Форма)
Функциональные и многозначные зависимости позволяют произвести декомпозицию исходного отношения без потерь на две проекции. Можно, однако, привести примеры отношений, которые нельзя декомпозировать без потерь ни на какие две проекции.
Нормальные формы более высоких порядков
Глава 7. Нормальные формы более высоких порядков
В предыдущей главе были рассмотрены нормальные формы вплоть до третьей нормальной формы (3НФ). В большинстве случаев этого вполне достаточно, чтобы разрабатывать вполне работоспособные базы данных. В данной главе рассматриваются нормальные формы более высоких порядков, а именно, нормальная форма Бойса-Кодда (НФБК), четвертая нормальная форма (4НФ), пятая нормальная форма (5НФ).
НФБК (Нормальная Форма Бойса-Кодда)
НФБК (Нормальная Форма Бойса-Кодда)
При приведении отношений при помощи алгоритма нормализации к отношениям в 3НФ неявно предполагалось, что все отношения содержат один потенциальный ключ. Это не всегда верно. Рассмотрим следующий пример отношения, содержащего два ключа.
и только тогда, когда детерминанты
Определение 1
. Отношение  нормальной форме Бойса-Кодда (НФБК) тогда и только тогда, когда детерминанты всех функциональных зависимостей являются потенциальными ключами.
Замечание. Если отношение находится в НФБК, то оно автоматически находится и в 3НФ. Действительно, это сразу следует из определения 3НФ.
Отношение "Поставки" не находится в НФБК, т.к. имеются зависимости (PNUM
нормальной форме Бойса-Кодда (НФБК) тогда и только тогда, когда детерминанты всех функциональных зависимостей являются потенциальными ключами.
Замечание. Если отношение находится в НФБК, то оно автоматически находится и в 3НФ. Действительно, это сразу следует из определения 3НФ.
Отношение "Поставки" не находится в НФБК, т.к. имеются зависимости (PNUM  PNAME и PNAME
PNAME и PNAME  PNUM), детерминанты которых не являются потенциальными ключами.
Для того чтобы устранить зависимость от детерминантов, не являющихся потенциальными ключами, необходимо провести декомпозицию, вынося эти детерминанты и зависимые от них части в отдельное отношение. Отношения "Поставщики" и "Поставки-2", полученные в результате декомпозиции находятся в НФБК.
Замечание. Приведенная декомпозиция отношения "Поставки" на отношения "Поставщики" и "Поставки-2" не является единственно возможной. Альтернативной декомпозицией является декомпозиция на следующие отношения:
PNUM), детерминанты которых не являются потенциальными ключами.
Для того чтобы устранить зависимость от детерминантов, не являющихся потенциальными ключами, необходимо провести декомпозицию, вынося эти детерминанты и зависимые от них части в отдельное отношение. Отношения "Поставщики" и "Поставки-2", полученные в результате декомпозиции находятся в НФБК.
Замечание. Приведенная декомпозиция отношения "Поставки" на отношения "Поставщики" и "Поставки-2" не является единственно возможной. Альтернативной декомпозицией является декомпозиция на следующие отношения:
и только тогда, когда из
Определение 2
. Пусть 
![]() ,
, 
![]() - некоторые из его атрибутов (или непересекающиеся множества атрибутов).
Тогда атрибуты (множества атрибутов)
- некоторые из его атрибутов (или непересекающиеся множества атрибутов).
Тогда атрибуты (множества атрибутов) 
![]() многозначно зависят от
многозначно зависят от 
![]() ), тогда и только тогда, когда из того, что в отношении
), тогда и только тогда, когда из того, что в отношении 
![]() и
и 
![]() содержится также и кортеж к
содержится также и кортеж к Замечание. Меняя местами кортежи
Замечание. Меняя местами кортежи 
![]() в определении многозначной зависимости, получим, что в отношении
в определении многозначной зависимости, получим, что в отношении 
![]() . Таким образом, атрибуты
. Таким образом, атрибуты 
![]() , многозначно зависящие от
, многозначно зависящие от 
![]() .
В отношении "Абитуриенты-Факультеты-Предметы" имеется многозначная зависимость Факультет
.
В отношении "Абитуриенты-Факультеты-Предметы" имеется многозначная зависимость Факультет Словами это можно выразить так - для каждого факультета (для каждого значения из
Словами это можно выразить так - для каждого факультета (для каждого значения из 
![]() ) сдает один и тот же список предметов (набор значений из
) сдает один и тот же список предметов (набор значений из 
![]() ) каждый сдаваемый на факультете экзамен (значение из
) каждый сдаваемый на факультете экзамен (значение из 
![]() ). Именно наличие этой зависимости не позволяет независимо вставлять и удалять кортежи. Кортежи обязаны вставляться и удаляться одновременно целыми наборами.
Замечание. Если в отношении
). Именно наличие этой зависимости не позволяет независимо вставлять и удалять кортежи. Кортежи обязаны вставляться и удаляться одновременно целыми наборами.
Замечание. Если в отношении 
![]() ,
, 
![]() и есть функциональная зависимость
и есть функциональная зависимость 
![]() .
Действительно, действуя формально в соответствии с определением многозначной зависимости, предположим, что в отношении
.
Действительно, действуя формально в соответствии с определением многозначной зависимости, предположим, что в отношении 
![]() и
и 
![]() отсюда следует, что
отсюда следует, что 
![]() в точности совпадает с кортежем
в точности совпадает с кортежем 
![]() . Таким образом, имеется многозначная зависимость
. Таким образом, имеется многозначная зависимость  Таким образом, понятие многозначной зависимости является обобщением понятия функциональной зависимости.
Таким образом, понятие многозначной зависимости является обобщением понятия функциональной зависимости.
если не существует функциональных зависимостей
Определение 3
. Многозначная зависимость  нетривиальной многозначной зависимостью, если не существует функциональных зависимостей
нетривиальной многозначной зависимостью, если не существует функциональных зависимостей 
![]() .
В отношении "Абитуриенты-Факультеты-Предметы" имеется именно нетривиальная многозначная зависимость Факультет
.
В отношении "Абитуриенты-Факультеты-Предметы" имеется именно нетривиальная многозначная зависимость Факультет
и только тогда, когда отношение
Определение 4
. Отношение  четвертой нормальной форме (4НФ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей.
Отношение "Абитуриенты-Факультеты-Предметы" находится в НФБК, но не в 4НФ. Согласно теореме Фейджина, это отношение можно без потерь декомпозировать на отношения:
четвертой нормальной форме (4НФ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей.
Отношение "Абитуриенты-Факультеты-Предметы" находится в НФБК, но не в 4НФ. Согласно теореме Фейджина, это отношение можно без потерь декомпозировать на отношения:
возможно пересекающимися) подмножествами множества атрибутов
Определение 5
. Пусть 
![]() ,
, 
![]() - произвольными ( возможно пересекающимися) подмножествами множества атрибутов отношения
- произвольными ( возможно пересекающимися) подмножествами множества атрибутов отношения 
![]() удовлетворяет зависимости соединения
удовлетворяет зависимости соединения
 тогда и только тогда, когда оно равносильно соединению всех своих проекций с подмножествами атрибутов
тогда и только тогда, когда оно равносильно соединению всех своих проекций с подмножествами атрибутов 
![]() , …,
, …, 
 Можно предположить, что отношение
Можно предположить, что отношение 
 Утверждать, что это именно так мы пока не можем, т.к. определение зависимости соединения должно выполняться для любого состояния отношения
Утверждать, что это именно так мы пока не можем, т.к. определение зависимости соединения должно выполняться для любого состояния отношения  Покажем, что зависимость соединения является обобщением понятия многозначной зависимости. Действительно, согласно теореме Фейджина, отношение
Покажем, что зависимость соединения является обобщением понятия многозначной зависимости. Действительно, согласно теореме Фейджина, отношение 
![]() и
и 
![]() . Согласно определению зависимости соединения, теорема Фейджина может быть переформулирована следующим образом:
. Согласно определению зависимости соединения, теорема Фейджина может быть переформулирована следующим образом:
Ни одно из множеств атрибутов
Определение 6
. Зависимость соединения  нетривиальной зависимостью соединения, если выполняется два условия:
Одно из множеств атрибутов
нетривиальной зависимостью соединения, если выполняется два условия:
Одно из множеств атрибутов 
![]() .
Ни одно из множеств атрибутов не совпадает со всем множеством атрибутов отношения
.
Ни одно из множеств атрибутов не совпадает со всем множеством атрибутов отношения  Для удобства работы сформулируем это определение так же и в отрицательной форме:
Для удобства работы сформулируем это определение так же и в отрицательной форме:
Либо одно из множеств атрибутов
Определение 7
. Зависимость соединения  тривиальной зависимостью соединения, если выполняется одно из условий:
Либо все множества атрибутов
тривиальной зависимостью соединения, если выполняется одно из условий:
Либо все множества атрибутов 
![]() .
Либо одно из множеств атрибутов совпадает со всем множеством атрибутов отношения
.
Либо одно из множеств атрибутов совпадает со всем множеством атрибутов отношения 
и только тогда, когда любая
Определение 8
. Отношение  пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной.
Определения 5НФ может стать более понятным, если сформулировать его в отрицательной форме:
пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной.
Определения 5НФ может стать более понятным, если сформулировать его в отрицательной форме:
в отношении найдется нетривиальная зависимость
Определение 9
. Отношение  5НФ, если в отношении найдется нетривиальная зависимость соединения.
Возвращаясь к примеру 3, становится понятно, что не зная ничего о том, какие потенциальные ключи имеются в отношении и как взаимосвязаны атрибуты, нельзя делать выводы о том, находится ли данное отношение в 5НФ (как, впрочем, и в других нормальных формах). По данному конкретному примеру можно только предположить, что отношение в примере 3 не находится в 5НФ. Предположим, что анализ предметной области позволил выявить следующие зависимости атрибутов в отношении
5НФ, если в отношении найдется нетривиальная зависимость соединения.
Возвращаясь к примеру 3, становится понятно, что не зная ничего о том, какие потенциальные ключи имеются в отношении и как взаимосвязаны атрибуты, нельзя делать выводы о том, находится ли данное отношение в 5НФ (как, впрочем, и в других нормальных формах). По данному конкретному примеру можно только предположить, что отношение в примере 3 не находится в 5НФ. Предположим, что анализ предметной области позволил выявить следующие зависимости атрибутов в отношении  (i) Отношение
(i) Отношение  (ii) Имеется следующая зависимость (довольно странная, с практической точки зрения): если в отношении
(ii) Имеется следующая зависимость (довольно странная, с практической точки зрения): если в отношении 
![]() ,
, 
![]() , то отсюда следует, что в отношении
, то отсюда следует, что в отношении 
![]() .
Утверждение. Докажем, что при наличии ограничений (i) и (ii), отношение находится в 4НФ, но не в 5НФ.
Доказательство. Покажем, что отношение
.
Утверждение. Докажем, что при наличии ограничений (i) и (ii), отношение находится в 4НФ, но не в 5НФ.
Доказательство. Покажем, что отношение  Покажем, что отношение не находится в 5НФ. Для этого нужно привести пример нетривиальной зависимости соединения. Естественным кандидатом на нее является
Покажем, что отношение не находится в 5НФ. Для этого нужно привести пример нетривиальной зависимости соединения. Естественным кандидатом на нее является 
![]() ,
, 
![]() не совпадает с множеством всех атрибутов отношения
не совпадает с множеством всех атрибутов отношения  Но является ли такая декомпозиция именно зависимостью соединения? Для этого нужно показать, что декомпозиция на три проекции
Но является ли такая декомпозиция именно зависимостью соединения? Для этого нужно показать, что декомпозиция на три проекции 
![]() и
и 
![]() (именно здесь содержится ключевая тонкость, обычно пропускаемая при анализе конкретного состояния отношения
(именно здесь содержится ключевая тонкость, обычно пропускаемая при анализе конкретного состояния отношения  Как и в предыдущих доказательствах, нужно доказать, что
Как и в предыдущих доказательствах, нужно доказать, что 
![]() .
Включение
.
Включение 
![]() .
Докажем включение
.
Докажем включение  Пусть кортеж
Пусть кортеж 
![]() содержится кортеж
содержится кортеж 
![]() содержится кортеж
содержится кортеж 
![]() содержится кортеж
содержится кортеж 
![]() ,
, 
![]() атрибутов
атрибутов 
![]() и
и 
![]() содержит кортежи
содержит кортежи 
![]() и
и 
![]() содержится также и кортеж
содержится также и кортеж  Утверждение доказано.
Утверждение доказано.
о поставках деталей некоторыми поставщиками.
Пример 1
. Пусть требуется хранить данные о поставках деталей некоторыми поставщиками. Предположим, что наименования поставщиков являются уникальными. Кроме того, каждый поставщик имеет свой уникальный номер. Данные о поставках можно хранить в следующем отношении:
прежнему необходимо учитывать поставки, но
Пример 2
. Предположим, что нам по- прежнему необходимо учитывать поставки, но каждый акт поставки должен иметь некоторый уникальный номер (назовем его "сквозной номер поставки"). Отношение может иметь следующий вид:
Рассмотрим следующее отношение
Пример 3
. Рассмотрим следующее отношение 
Продолжение алгоритма нормализации (приведение к 5НФ)
Продолжение алгоритма нормализации (приведение к 5НФ)
В предыдущей главе был описан алгоритм нормализации как алгоритм приведения отношений к 3НФ. Теперь мы можем продолжить этот алгоритм, доведя его до алгоритма приведения к 5НФ.
Приведение к НФБК)
Шаг 4 (Приведение к НФБК)
. Если имеются отношения, содержащие несколько потенциальных ключей, то необходимо проверить, имеются ли функциональные зависимости, детерминанты которых не являются потенциальными ключами. Если такие функциональные зависимости имеются, то необходимо провести дальнейшую декомпозицию отношений. Те атрибуты, которые зависят от детерминантов, не являющихся потенциальными ключами выносятся в отдельное отношение вместе с детерминантами.
Приведение к 4НФ)
Шаг 5 (Приведение к 4НФ)
. Если в отношениях обнаружены нетривиальные многозначные зависимости, то необходимо провести декомпозицию для исключения таких зависимостей.
Приведение к 5НФ)
Шаг 5 (Приведение к 5НФ)
. Если в отношениях обнаружены нетривиальные зависимости соединения, то необходимо провести декомпозицию для исключения и таких зависимостей.
Данное отношение содержит два потенциальных
Таблица 1
| 1 | Фирма 1 | 1 | 100 |
| 1 | Фирма 1 | 2 | 200 |
| 1 | Фирма 1 | 3 | 300 |
| 2 | Фирма 2 | 1 | 150 |
| 2 | Фирма 2 | 2 | 250 |
| 3 | Фирма 3 | 1 | 1000 |
Таблица 1 Отношение "Поставки"
Данное отношение содержит два потенциальных ключа - {PNUM, DNUM} и {PNAME, DNUM}. Видно, что данные хранятся в отношении с избыточностью - при изменении наименования поставщика, это наименование нужно изменить во всех кортежах, где оно встречается. Можно ли эту аномалию устранить при помощи алгоритма нормализации, описанного в предыдущей главе? Для этого нужно выявить имеющиеся функциональные зависимости (как обычно, курсивом выделены ключевые атрибуты):
PNUM  PNAME - наименование поставщика зависит от номера поставщика.
PNAME
PNAME - наименование поставщика зависит от номера поставщика.
PNAME  PNUM - номер поставщика зависит от наименования поставщика.
{PNUM, DNUM}
PNUM - номер поставщика зависит от наименования поставщика.
{PNUM, DNUM}  VOLUME - поставляемое количество зависит от первого ключа отношения.
{PNUM, DNUM}
VOLUME - поставляемое количество зависит от первого ключа отношения.
{PNUM, DNUM}  PNAME - наименование поставщика зависит от первого ключа отношения.
{PNAME, DNUM}
PNAME - наименование поставщика зависит от первого ключа отношения.
{PNAME, DNUM}  VOLUME - поставляемое количество зависит от второго ключа отношения.
{PNAME, DNUM}
VOLUME - поставляемое количество зависит от второго ключа отношения.
{PNAME, DNUM}  PNUM - номер поставщика зависит от второго ключа отношения.
Данное отношение не содержит неключевых атрибутов, зависящих от части сложного ключа (см. определение 2НФ). Действительно, от части сложного ключа зависят атрибуты PNAME и PNUM, но они сами являются ключевыми. Таким образом, отношение находится в 2НФ.
Кроме того, отношение не содержит зависимых друг от друга неключевых атрибутов, т.к. неключевой атрибут всего один - VOLUME (см. определение 3НФ). Таким образом, показано, что отношение "Поставки" находится в 3НФ.
Таким образом, описанный ранее алгоритм нормализации неприменим к данному отношению. Очевидно, однако, что аномалия данного отношения устраняется путем декомпозиции его на два следующих отношения:
PNUM - номер поставщика зависит от второго ключа отношения.
Данное отношение не содержит неключевых атрибутов, зависящих от части сложного ключа (см. определение 2НФ). Действительно, от части сложного ключа зависят атрибуты PNAME и PNUM, но они сами являются ключевыми. Таким образом, отношение находится в 2НФ.
Кроме того, отношение не содержит зависимых друг от друга неключевых атрибутов, т.к. неключевой атрибут всего один - VOLUME (см. определение 3НФ). Таким образом, показано, что отношение "Поставки" находится в 3НФ.
Таким образом, описанный ранее алгоритм нормализации неприменим к данному отношению. Очевидно, однако, что аномалия данного отношения устраняется путем декомпозиции его на два следующих отношения:
Отношение "Поставщики"
Таблица 2
Таблица 2 Отношение "Поставщики"
Отношение "Поставки-2"
Таблица 3
| 1 | 1 | 100 |
| 1 | 2 | 200 |
| 1 | 3 | 300 |
| 2 | 1 | 150 |
| 2 | 2 | 250 |
| 3 | 1 | 1000 |
Таблица 3 Отношение "Поставки-2"
Отношение "Поставщики"
Таблица 4
Таблица 4 Отношение "Поставщики"
На первый взгляд, такая декомпозиция
Таблица 5
| 1 | 100 |
| 2 | 200 |
| 3 | 300 |
| 1 | 150 |
| 2 | 250 |
| 1 | 1000 |
Таблица 5 Отношение "Поставки-3"
На первый взгляд, такая декомпозиция хуже, чем первая. Действительно, наименования поставщиков по-прежнему повторяются, и при изменении наименования поставщика, это наименование придется менять одновременно в нескольких местах (тем более сразу в двух отношениях!). Кажется, что ситуация стала еще хуже, чем была до декомпозиции. Однако такое ощущение возникает от того, что мы интуитивно считаем, что наименования поставщиков могут меняться, а номера - нет. Если же предположить, что номера поставщиков тоже могут меняться (почему бы нет - директор приказал перенумеровать поставщиков!), то первая декомпозиция получается такой же "плохой" как и вторая - повторяющиеся номера придется менять одновременно в нескольких местах и также сразу в двух отношениях.
На самом деле никакого противоречия тут нет. В отношении "Поставки-3" атрибут "Наименование поставщика" (PNAME) является внешним ключом, служащим для связи с отношением "Поставщики". Поэтому, при изменении наименования поставщика, это изменение производится в отношении "Поставщики" и каскадно (см. стратегии поддержания ссылочной целостности в гл. 3) распространяется на отношение "Поставки-3" совершенно так, как изменение номера поставщика каскадно распространяется на отношение "Поставки-2". Поэтому, формально обе декомпозиции совершенно равноправны. В реальной работе разработчик выберет, конечно, первую декомпозицию, но тут важно подчеркнуть, что его выбор основан совсем на других соображениях, не имеющих отношения к формальной теории нормальных форм.
Замечание. Отношение "Поставки-2", полученное в результате декомпозиции имеет всего один потенциальный ключ. Поэтому, для анализа отношения "Поставки-2" не требуется привлекать определение НФБК, достаточно определения 3НФ. Хотя отношение "Поставщики" имеет два потенциальных ключа, но, т.к. других атрибутов в нем нет, оно уже так просто устроено, что упростить его дальше нельзя. Возникает вопрос, имеются ли нетривиальные примеры отношений в НФБК, не находящиеся в 3НФ и не такие простые, как отношение "Поставщики"?
Одним потенциальным ключом данного отношения
Таблица 6
Номер поставщика
PNUMНомер детали
DNUMПоставляемое количество
VOLUMEСквозной номер поставки
NN
1
1
100
1
1
2
200
2
1
3
300
3
2
1
150
4
2
2
250
5
3
1
1000
6
Таблица 6 Отношение "Поставки-с-номером"
Одним потенциальным ключом данного отношения является, как и раньше, пара атрибутов {PNUM, DNUM}. Другим ключом, в силу уникальности сквозного номера, является атрибут NN. В данном отношении имеются следующие функциональные зависимости:
Зависимость атрибутов от первого ключа отношения:
{PNUM, DNUM}  VOLUME,
{PNUM, DNUM}
VOLUME,
{PNUM, DNUM}  NN,
Зависимость атрибутов от второго ключа отношения:
NN
NN,
Зависимость атрибутов от второго ключа отношения:
NN  PNUM,
NN
PNUM,
NN  DNUM,
NN
DNUM,
NN  VOLUME,
Зависимости, являющиеся следствием зависимостей от ключей отношения:
{PNUM, DNUM}
VOLUME,
Зависимости, являющиеся следствием зависимостей от ключей отношения:
{PNUM, DNUM}  VOLUME, NN},
NN
VOLUME, NN},
NN  {PNUM, DNUM},
NN
{PNUM, DNUM},
NN  {PNUM, VOLUME},
NN
{PNUM, VOLUME},
NN  {DNUM, VOLUME},
NN
{DNUM, VOLUME},
NN  {PNUM, DNUM, VOLUME}.
Как можно заметить, детерминанты всех зависимостей являются потенциальными ключами, поэтому данное отношение находится в НФБК. Особенностью данного отношения является то, что оно имеет два совершенно независимых потенциальных ключа.
{PNUM, DNUM, VOLUME}.
Как можно заметить, детерминанты всех зависимостей являются потенциальными ключами, поэтому данное отношение находится в НФБК. Особенностью данного отношения является то, что оно имеет два совершенно независимых потенциальных ключа.
о том, что абитуриент Иванов
Таблица 7
| Иванов | Математический | Математика |
| Иванов | Математический | Информатика |
| Иванов | Физический | Математика |
| Иванов | Физический | Физика |
| Петров | Математический | Математика |
| Петров | Математический | Информатика |
Таблица 7 Отношение "Абитуриенты-Факультеты-Предметы"
В данный момент в отношении хранится информация о том, что абитуриент Иванов поступает на два факультета (математически и физический), а абитуриент Петров - только на математический. Кроме того, можно сделать вывод, что на математическом факультете нужно сдавать математику и информатику, а на физическом - математику и физику.
Кажется, что в отношении имеется аномалия обновления, связанная с тем, что дублируются фамилии абитуриентов, наименования факультетов и наименования предметов. Однако эта аномалия легко устраняется стандартным способом - вынесением всех наименований в отдельные отношения, оставляя в исходном отношении только соответствующие номера:
Модифицированное отношение
Таблица 8
| 1 | 1 | 1 |
| 1 | 1 | 2 |
| 1 | 2 | 1 |
| 1 | 2 | 3 |
| 2 | 1 | 1 |
| 2 | 1 | 2 |
Таблица 8 Модифицированное отношение "Абитуриенты-Факультеты-Предметы"
Отношение "Абитуриенты"
Таблица 9
| 1 | Иванов |
| 2 | Петров |
Таблица 9 Отношение "Абитуриенты"
center> Таблица
Таблица 10
| 1 | Математический |
| 2 | Физический |
Таблица 10 Отношение "Факультеты"
Теперь каждое наименование встречается только
Таблица 11
| 1 | Математика |
| 2 | Информатика |
| 3 | Физика |
Таблица 11 Отношение "Предметы"
Теперь каждое наименование встречается только в одном месте.
И все-таки как в исходном, так и в модифицированном отношении имеются аномалии обновления, возникающие при попытке вставить или удалить кортежи.
Аномалия вставки. При попытке добавить в отношение "Абитуриенты-Факультеты-Предметы" новый кортеж, например (Сидоров, Математический, Математика), мы обязаны добавить также и кортеж (Сидоров, Математический, Информатика), т.к. все абитуриенты математического факультета обязаны иметь один и тот же список сдаваемых предметов. Соответственно, при попытке вставить в модифицированное отношении кортеж (3, 1, 1), мы обязаны вставить в него также и кортеж (3, 1, 2).
Аномалия удаления. При попытке удалить кортеж (Иванов, Математический, Математика), мы обязаны удалить также и кортеж (Иванов, Математический, Информатика) по той же самой причине.
Таким образом, вставка и удаление кортежей не может быть выполнена независимо от других кортежей отношения.
Кроме того, если мы удалим кортеж (Иванов, Физический, Математика), а вместе с ним и кортеж (Иванов, Физический, Физика), то будет потеряна информация о предметах, которые должны сдаваться на физическом факультете.
Декомпозиция отношения "Абитуриенты-Факультеты-Предметы" для устранения указанных аномалий не может быть выполнена на основе функциональных зависимостей, т.к. это отношение не содержит никаких функциональных зависимостей. Это отношение является полностью ключевым, т.е. ключом отношения является все множество атрибутов. Но ясно, что какая-то взаимосвязь между атрибутами имеется. Эта взаимосвязь описывается понятием многозначной зависимости.
center> Таблица
Таблица 12
| Математический | Иванов |
| Физический | Иванов |
| Математический | Петров |
Таблица 12 Отношение "Факультеты-Абитуриенты"
В полученных отношениях устранены аномалии
Таблица 13
| Математический | Математика |
| Математический | Информатика |
| Физический | Математика |
| Физический | Физика |
Таблица 13 Отношение "Факультеты-Предметы"
В полученных отношениях устранены аномалии вставки и удаления, характерные для отношения "Абитуриенты-Факультеты-Предметы".
Заметим, что полученные отношения остались полностью ключевыми, и в них по-прежнему нет функциональных зависимостей.
Отношения с нетривиальными многозначными зависимостями возникают, как правило, в результате естественного соединения двух отношений по общему полю, которое не является ключевым ни в одном из отношений. Фактически это приводит к попытке хранить в одном отношении информацию о двух независимых сущностях. В качестве еще одного примера можно привести ситуацию, когда сотрудник может иметь много работ и много детей. Хранение информации о работах и детях в одном отношении приводит к возникновению нетривиальной многозначной зависимости Работник
center> Таблица
Таблица 14
| 1 | 1 | 2 |
| 1 | 2 | 1 |
| 2 | 1 | 1 |
| 1 | 1 | 1 |
Таблица 14 Отношение R
Всевозможные проекции отношения 
center> Таблица
Таблица 15
| 1 | 1 |
| 1 | 2 |
| 2 | 1 |
Таблица 15 Проекция R1=R[X,Y]
center> Таблица
Таблица 16
| 1 | 2 |
| 1 | 1 |
| 2 | 1 |
Таблица 16 Проекция R2=R[X,Z]
Как легко заметить, отношение
Таблица 17
| 1 | 2 |
| 2 | 1 |
| 1 | 1 |
Таблица 17 Проекция R3=R[Y,Z]
Как легко заметить, отношение 
![]() ,
, 
![]() . Действительно, соединение
. Действительно, соединение 
Серым цветом выделен лишний кортеж,
Таблица 18
| 1 | 1 | 2 |
| 1 | 1 | 1 |
| 1 | 2 | 2 |
| 1 | 2 | 1 |
| 2 | 1 | 1 |
Таблица 18 R1 JOIN R2
Серым цветом выделен лишний кортеж, отсутствующий в отношении 
![]() .
Однако отношение
.
Однако отношение 
 Это говорит о том, что между атрибутами этого отношения также имеется некоторая зависимость, но эта зависимость не является ни функциональной, ни многозначной зависимостью.
Это говорит о том, что между атрибутами этого отношения также имеется некоторая зависимость, но эта зависимость не является ни функциональной, ни многозначной зависимостью.
Теорема (Фейджина)
Теорема (Фейджина)
. Пусть


Декомпозиция отношения 
![]() и
и 
![]() .
.
Замечание. Если зависимость 
![]() или
или 
Доказательство теоремы.
Необходимость. Пусть декомпозиция отношения 
![]() и
и 
![]() .
.
Предположим, что отношение 
![]() и
и 
![]() также содержится в
также содержится в 
![]() содержится в
содержится в 
![]() содержится в
содержится в 
![]() содержится в естественном соединении
содержится в естественном соединении 
![]() . Необходимость доказана.
. Необходимость доказана.
Достаточность. Пусть имеется многозначная зависимость 
![]() на проекции
на проекции 
![]() является декомпозицией без потерь.
является декомпозицией без потерь.
Как и в доказательстве теоремы Хеза, нужно доказать, что 
![]() .
.
Включение 
![]() .
.
Докажем включение 
![]() . Это означает, что в проекции
. Это означает, что в проекции 
![]() , а в проекции
, а в проекции 
![]() . По определению проекции, найдется такое значение
. По определению проекции, найдется такое значение 
![]() , что отношение
, что отношение 
![]() . Аналогично, найдется такое значение
. Аналогично, найдется такое значение 
![]() , что отношение
, что отношение 
![]() . Тогда по определению многозначной зависимости кортеж
. Тогда по определению многозначной зависимости кортеж  Достаточность доказана.
Достаточность доказана.
Теорема Фейджина (другая формулировка)
Теорема Фейджина (другая формулировка)
. Отношение 
![]() тогда и только тогда, когда имеется многозначная зависимость
тогда и только тогда, когда имеется многозначная зависимость 
Т.к. теорема Фейджина является взаимно обратной, то ее можно взять в качестве определения многозначной зависимости. Таким образом, многозначная зависимость является частным случаем зависимости соединения, т.е., если в отношении имеется многозначная зависимость, то имеется и зависимость соединения. Обратное, конечно, неверно.
Обобщением 3НФ на случай, когда
Выводы
Обобщением 3НФ на случай, когда отношение имеет более одного потенциального ключа, является нормальная форма Бойса-Кодда. Отношение
 нормальной форме Бойса-Кодда (НФБК) тогда и только тогда, когда детерминанты всех функциональных зависимостей являются потенциальными ключами.
Нормализация отношений вплоть до нормальной формы Бойса-Кодда основывалась на понятии функциональной зависимости и теореме Хеза, гарантировавшей, что декомпозиция будет происходить без потерь информации.
Дальнейшая нормализация связана уже с обобщением понятия функциональной зависимости.
Атрибуты (множества атрибутов)
нормальной форме Бойса-Кодда (НФБК) тогда и только тогда, когда детерминанты всех функциональных зависимостей являются потенциальными ключами.
Нормализация отношений вплоть до нормальной формы Бойса-Кодда основывалась на понятии функциональной зависимости и теореме Хеза, гарантировавшей, что декомпозиция будет происходить без потерь информации.
Дальнейшая нормализация связана уже с обобщением понятия функциональной зависимости.
Атрибуты (множества атрибутов) 



 Корректность дальнейшей декомпозиции основывается на теореме Фейджина, которая говорит о том, что декомпозиция отношения на две проекции является декомпозицией без потерь тогда и только тогда, когда в отношении имеется некоторая многозначная зависимость.
Если в отношении имеется функциональная зависимость, то автоматически имеется и тривиальная многозначная зависимость, определяемая этой функциональной зависимостью.
Многозначная зависимость
Корректность дальнейшей декомпозиции основывается на теореме Фейджина, которая говорит о том, что декомпозиция отношения на две проекции является декомпозицией без потерь тогда и только тогда, когда в отношении имеется некоторая многозначная зависимость.
Если в отношении имеется функциональная зависимость, то автоматически имеется и тривиальная многозначная зависимость, определяемая этой функциональной зависимостью.
Многозначная зависимость 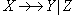 нетривиальной многозначной зависимостью, если не существует функциональных зависимостей
нетривиальной многозначной зависимостью, если не существует функциональных зависимостей 
 четвертой нормальной форме (4НФ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей.
Имеют место зависимости специального вида, когда отношение не может быть подвергнуто декомпозиции без потерь на две проекции, но может быть декомпозировано на большее число проекций. Такие зависимости называются зависимостями соединения и являются обобщением понятия многозначной зависимости.
Отношение
четвертой нормальной форме (4НФ) тогда и только тогда, когда отношение находится в НФБК и не содержит нетривиальных многозначных зависимостей.
Имеют место зависимости специального вида, когда отношение не может быть подвергнуто декомпозиции без потерь на две проекции, но может быть декомпозировано на большее число проекций. Такие зависимости называются зависимостями соединения и являются обобщением понятия многозначной зависимости.
Отношение  пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной.
пятой нормальной форме (5НФ) тогда и только тогда, когда любая имеющаяся зависимость соединения является тривиальной.
