Введение в системы управления базами данных
Декартово произведение множеств
Декартово произведение множеств
Одним из способов конструирования новых объектов из уже имеющихся множеств является декартово произведение множеств.
Пусть 
![]() - множества. Выражение вида
- множества. Выражение вида 
![]() и
и 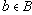 упорядоченной парой. Равенство вида
упорядоченной парой. Равенство вида 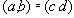
![]() и
и 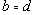 упорядоченную n-ку
упорядоченную n-ку 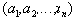
![]() . Упорядоченные n-ки иначе называют наборы или кортежи.
. Упорядоченные n-ки иначе называют наборы или кортежи.
Множества
Множества
Наиболее простая структура данных, используемая в математике, имеет место в случае, когда между отдельными изолированными данными отсутствуют какие-либо взаимосвязи. Совокупность таких данных представляет собой множество. Понятие множества является неопределяемым понятием. Множество не обладает внутренней структурой. Множество можно представить себе как совокупность элементов, обладающих некоторым общим свойством. Для того чтобы некоторую совокупность элементов можно было назвать множеством, необходимо, чтобы выполнялись следующие условия: Должно существовать правило, позволяющее определить, принадлежит ли указанный элемент данной совокупности. Должно существовать правило, позволяющее отличать элементы друг от друга. (Это, в частности, означает, что множество не может содержать двух одинаковых элементов).
Множества обычно обозначаются заглавными латинскими буквами. Если элемент 
![]() , то это обозначается:
, то это обозначается:
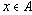
Если каждый элемент множества 
![]() , то говорят, что множество
, то говорят, что множество  подмножеством множества
подмножеством множества 
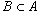
Подмножество 
![]() называется собственным подмножеством, если
называется собственным подмножеством, если
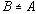
Используя понятие множества можно построить более сложные и содержательные объекты.
n-арные отношения (отношения степени n)
n-арные отношения (отношения степени n)
В математике n-арные отношения рассматриваются относительно редко, в отличие от баз данных, где наиболее важными являются именно отношения, заданные на декартовом произведении более чем двух множеств.
Операции над множествами
Операции над множествами
Основными операциями над множествами являются объединение, пересечение и разность.
двух множеств называется новое
Определение 1
. Объединением двух множеств называется новое множество
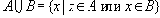
двух множеств называется новое
Определение 2
. Пересечением двух множеств называется новое множество
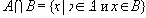
Если класс объектов, на которых
Определение 3
. Разностью двух множеств называется новое множество
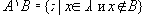 Если класс объектов, на которых определяются различные множества обозначить
Если класс объектов, на которых определяются различные множества обозначить  Универсум), то дополнением множества
Универсум), то дополнением множества 
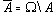
произведением множеств
Определение 4
. Декартовым (прямым) произведением множеств
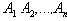
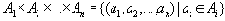
Если все множества
Определение 5
. Степенью декартового произведения
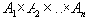 Замечание. Если все множества
Замечание. Если все множества 
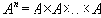
Определение 6"
Определение 6
. Подмножество

Понятие отношения является очень важным
Определение 7
. Мощность множества кортежей, входящих в отношение
 мощностью отношения
мощностью отношения  Замечание. Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей реляционной теории баз данных. Как будет показано ниже, отношения являются математическим аналогом таблиц. Сам термин "реляционное представление данных", впервые введенный Коддом [43], происходит от термина relation, понимаемом именно в смысле этого определения.
Т.к. любое множество можно рассматривать как декартовое произведение степени 1, то любое подмножество, как и любое множество, можно считать отношением степени 1. Это не очень интересный пример, свидетельствующий лишь о том, что термины "отношение степени 1" и "подмножество" являются синонимами. Нетривиальность понятия отношения проявляется, когда степень отношения больше 1. Ключевыми здесь являются два момента:
Во-первых, все элементы отношения есть однотипные кортежи. Однотипность кортежей позволяет считать их аналогами строк в простой таблице, т.е. в такой таблице, в которой все строки состоят из одинакового числа ячеек и в соответствующих ячейках содержатся одинаковые типы данных. Например, отношение, состоящее из трех следующих кортежей {(1, "Иванов", 1000), (2, "Петров", 2000), (3, "Сидоров", 3000)} можно считать таблицей, содержащей данные о сотрудниках и их зарплатах. Такая таблица будет иметь три строки и три колонки, причем в каждой колонке содержатся данные одного типа.
В противоположность этому рассмотрим множество {(1), (1, 2), (1, 2, 3)}, состоящее из разнотипных числовых кортежей. Это множество не является отношением ни в
Замечание. Понятие отношения является очень важным не только с математической точки зрения. Понятие отношения фактически лежит в основе всей реляционной теории баз данных. Как будет показано ниже, отношения являются математическим аналогом таблиц. Сам термин "реляционное представление данных", впервые введенный Коддом [43], происходит от термина relation, понимаемом именно в смысле этого определения.
Т.к. любое множество можно рассматривать как декартовое произведение степени 1, то любое подмножество, как и любое множество, можно считать отношением степени 1. Это не очень интересный пример, свидетельствующий лишь о том, что термины "отношение степени 1" и "подмножество" являются синонимами. Нетривиальность понятия отношения проявляется, когда степень отношения больше 1. Ключевыми здесь являются два момента:
Во-первых, все элементы отношения есть однотипные кортежи. Однотипность кортежей позволяет считать их аналогами строк в простой таблице, т.е. в такой таблице, в которой все строки состоят из одинакового числа ячеек и в соответствующих ячейках содержатся одинаковые типы данных. Например, отношение, состоящее из трех следующих кортежей {(1, "Иванов", 1000), (2, "Петров", 2000), (3, "Сидоров", 3000)} можно считать таблицей, содержащей данные о сотрудниках и их зарплатах. Такая таблица будет иметь три строки и три колонки, причем в каждой колонке содержатся данные одного типа.
В противоположность этому рассмотрим множество {(1), (1, 2), (1, 2, 3)}, состоящее из разнотипных числовых кортежей. Это множество не является отношением ни в 

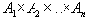 Действительно, каждому отношению можно поставить в соответствие некоторое логическое выражение
Действительно, каждому отношению можно поставить в соответствие некоторое логическое выражение 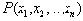
 предикатом отношения
предикатом отношения 


Обычно отношение эквивалентности обозначают знаком
Определение 8
. Отношение

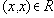
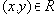
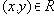
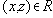 Обычно отношение эквивалентности обозначают знаком
Обычно отношение эквивалентности обозначают знаком 

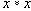
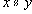
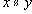
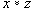 Легко доказывается, что если на множестве
Легко доказывается, что если на множестве 
Обычно отношение порядка обозначают знаком
Определение 9
. Отношение

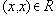
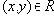
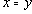 Если
Если 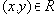
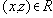 Обычно отношение порядка обозначают знаком
Обычно отношение порядка обозначают знаком 


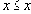
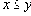
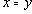 Если
Если 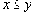
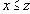
Предикат функционального отношения есть просто
Определение 10
. Отношение

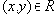
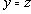 Обычно, функциональное отношение обозначают в виде функциональной зависимости -
Обычно, функциональное отношение обозначают в виде функциональной зависимости - 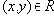
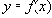
Определение 11.
Определение 11.
Пусть отношение

 Транзитивным замыканием отношения
Транзитивным замыканием отношения 
 либо кортеж
либо кортеж 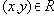 либо найдется конечная последовательность элементов
либо найдется конечная последовательность элементов 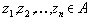

Очевидно, что 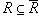
Рассмотрим на множестве вещественных чисел
Пример 1
. Рассмотрим на множестве вещественных чисел 
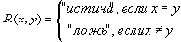
![]() Условия 1-3, очевидно, выполняются, поэтому данное отношение является отношением эквивалентности. Каждый класс эквивалентности этого отношения состоит из одного числа.
Условия 1-3, очевидно, выполняются, поэтому данное отношение является отношением эквивалентности. Каждый класс эквивалентности этого отношения состоит из одного числа.
Рассмотрим более сложное отношение эквивалентности.
Пример 2
. Рассмотрим более сложное отношение эквивалентности. На множестве целых чисел 
![]() и
и  равны по модулю n, если их остатки при делении на n равны. Например, по модулю 5 равны числа 2, 7, 12 и т.д.
Условия 1-3 легко проверяются, поэтому равенство по модулю является отношением эквивалентности. Предикат этого отношения имеет вид:
равны по модулю n, если их остатки при делении на n равны. Например, по модулю 5 равны числа 2, 7, 12 и т.д.
Условия 1-3 легко проверяются, поэтому равенство по модулю является отношением эквивалентности. Предикат этого отношения имеет вид:
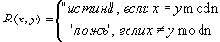 Классы эквивалентности этого отношения состоят из чисел, дающих при делении на n одинаковые остатки. Таких классов ровно n:
[0] = {0, n, 2n, …}
[1] = {1, n+1, 2n+1, …}[n-1] = {n-1, n+n-1, 2n+n-1, …}
Классы эквивалентности этого отношения состоят из чисел, дающих при делении на n одинаковые остатки. Таких классов ровно n:
[0] = {0, n, 2n, …}
[1] = {1, n+1, 2n+1, …}[n-1] = {n-1, n+n-1, 2n+n-1, …}
Простым примером отношения порядка является
Пример 3
. Простым примером отношения порядка является отношение, задаваемое обычным неравенством


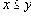
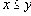
быть начальником" является отношением порядка.
Пример 4
. Рассмотрим на множестве


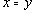


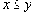

о взаимоотношения данных молодых людей
Пример 5
. Пусть множество
 Вовочка любит Вовочку (эгоист).
Петя любит Машу (взаимно).
Маша любит Петю (взаимно).
Маша любит Машу (себя не забывает).
Лена любит Петю (несчастная любовь).
Информацию о взаимоотношения данных молодых людей можно описать бинарным отношением "любить", заданном на множестве
Вовочка любит Вовочку (эгоист).
Петя любит Машу (взаимно).
Маша любит Петю (взаимно).
Маша любит Машу (себя не забывает).
Лена любит Петю (несчастная любовь).
Информацию о взаимоотношения данных молодых людей можно описать бинарным отношением "любить", заданном на множестве  Способ 1. Перечисление фактов в виде произвольного текста (как это сделано выше).
Способ 2. В виде графа взаимоотношений:
Способ 1. Перечисление фактов в виде произвольного текста (как это сделано выше).
Способ 2. В виде графа взаимоотношений: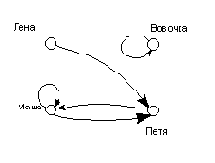
Рисунок 1 Граф взаимоотношений
Способ 3. При помощи матрицы взаимоотношений:
В некотором университете на математическом
Пример 6
. В некотором университете на математическом факультете учатся студенты Иванов, Петров и Сидоров. Лекции им читают преподаватели Пушников, Цыганов и Шарипов, причем известны следующие факты: Пушников читает лекции по алгебре и базам данных, соответственно, 40 и 80 часов в семестр. Цыганов читает лекции по геометрии, 50 часов в семестр. Шарипов читает лекции по алгебре и геометрии, соответственно, 40 и 50 часов в семестр. Студент Иванов посещает лекции по алгебре у Шарипова и по базам данных у Пушникова. Студент Петров посещает лекции по алгебре у Пушникова и по геометрии у Цыганова. Студент Сидоров посещает лекции по геометрии у Цыганова и по базам данных у Пушникова. Для того чтобы формально описать данную ситуацию (например, в целях разработки информационной системы, учитывающей данные о ходе учебного процесса), введем три множества: Множество преподавателей
 Множество предметов
Множество предметов  Множество студентов
Множество студентов  Имеющиеся факты можно разделить на две группы. 1 группа (факты 1-3) - факты о преподавателях, 2 группа (факты 4-6) - факты о студентах.
Для того чтобы отразить факты 1-3 (характеризующие преподавателей и читаемые ими лекции), введем отношение
Имеющиеся факты можно разделить на две группы. 1 группа (факты 1-3) - факты о преподавателях, 2 группа (факты 4-6) - факты о студентах.
Для того чтобы отразить факты 1-3 (характеризующие преподавателей и читаемые ими лекции), введем отношение 



и конструкций могут использоваться при
Пример 7
. Пусть множество

 причем некоторые из деталей и конструкций могут использоваться при сборке других конструкций. Взаимосвязь деталей описывается отношением
причем некоторые из деталей и конструкций могут использоваться при сборке других конструкций. Взаимосвязь деталей описывается отношением 
Примеры отношений Бинарные отношения (отношения степени 2)
Бинарные отношения (отношения степени 2)
В математике большую роль играют бинарные отношения, т.е. отношения, заданные на декартовом произведении двух множеств 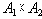
Матрица взаимоотношений
Таблица 1
|
Кого Кто |
Вовочка
Петя
Маша
Лена
|||
| Любит | |||
| Любит | |||
| Любит | Любит | ||
| Любит |
Таблица 1. Матрица взаимоотношенийСпособ 4. При помощи таблицы фактов:
Таблица фактовС точки зрения
Таблица 2
| Вовочка | Вовочка |
| Петя | Маша |
| Маша | Петя |
| Маша | Маша |
| Лена | Петя |
Таблица 2 Таблица фактовС точки зрения реляционных баз данных наиболее предпочтительным является четвертый способ, т.к. он допускает наиболее удобный способ хранения и манипулирования информацией. Действительно, перечисление фактов как текстовая форма хранения информации уместна для литературного произведения, но с трудом поддается алгоритмической обработке. Изображение в виде графа наглядно, и его удобно использовать как конечную форму представления информации для пользователя, но хранить данные в графическом виде неудобно. Матрица взаимоотношений уже больше соответствует требованиям информационной системы. Матрица удобна в обработке и компактно хранится. Но одно небольшое изменение, например, появился еще Вася и влюбился в несчастную Лену, требует перестройки всей матрицы, а именно, добавления и колонок, и столбцов. Таблица фактов свободна от всех этих недостатков - при добавлении новых действующих лиц просто добавляются новые строки.
Что касается предиката данного отношения, то он имеет следующий вид (дизъюнктивная нормальная форма):
R(x,y) = {(x = "Вовочка" AND y = "Вовочка") OR (x = "Петя" AND y = "Маша") OR (x = "Маша" AND y = "Петя") OR (x = "Маша" AND y = "Маша") OR (x = "Лена" AND y = "Петя")}
Замечание. Приведенное отношение не является ни транзитивным, ни симметричным или антисимметричным, ни рефлексивным, поэтому оно не является ни отношением эквивалентности, ни отношением порядка, ни каким-либо другим разумным отношением.
Замечание. Большая часть мировой литературы существует и имеет смысл лишь постольку, поскольку бинарное отношение "любить" не является отношением эквивалентности. В частности, по этой причине человечество не разбивается на классы эквивалентности взаимно любящих особей. Изучением характеристик данного отношения и соответствующего ему предиката занималось (и продолжает заниматься) большое количество экспертов, таких как Толстой Л.Н., Шекспир В. и др.
Для того чтобы отразить факты
Таблица 3
| Пушников | Алгебра | 40 |
| Пушников | Базы данных | 80 |
| Цыганов | Геометрия | 50 |
| Шарипов | Алгебра | 40 |
| Шарипов | Геометрия | 50 |
Таблица 3 Отношение "Читает лекции по…"
Для того чтобы отразить факты 4-6 (характеризующие посещение студентами лекций), введем отношение 
![]() . Упорядоченная тройка
. Упорядоченная тройка 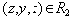
![]() посещает лекции по предмету
посещает лекции по предмету 
![]() . Назовем это отношение "Посещать лекции". Его также представим в виде таблицы:
. Назовем это отношение "Посещать лекции". Его также представим в виде таблицы:
показывает текущее состояние учебного процесса.
Таблица 4
| Иванов | Алгебра | Шарипов |
| Иванов | Базы данных | Пушников |
| Петров | Алгебра | Пушников |
| Петров | Геометрия | Цыганов |
| Сидоров | Геометрия | Цыганов |
| Сидоров | Базы данных | Пушников |
Таблица 4 Отношение "Посещать лекции"
Рассмотрим отношение 
![]() . Это произведение, содержащее 3*3*3=27 кортежей, можно назвать "Студенты-Лекции-Преподаватели". Множество
. Это произведение, содержащее 3*3*3=27 кортежей, можно назвать "Студенты-Лекции-Преподаватели". Множество 
![]() показывает текущее состояние учебного процесса. Очевидно, что отношение
показывает текущее состояние учебного процесса. Очевидно, что отношение  Итак, факты о ходе учебного процесса удалось отразить в виде двух отношений третьей степени (3-арных), а сами отношения изобразить в виде таблиц с тремя колонками.
Удобство использования табличной формы для задания отношения определяется в данном случае следующими факторами:
Все используемые множества конечны.
При добавлении или удалении студентов, предметов, преподавателей просто добавляются или удаляются соответствующие строки в таблице.
Нас сейчас не интересует вопрос, хороши ли полученные отношения. Заметим пока только, что, как показывают следующие замечания, не любую строку можно добавить в таблицу "Посещать лекции".
Замечание. В таблицу "Посещать лекции" нельзя добавить две одинаковые строки, т.к. таблица изображает отношение
Итак, факты о ходе учебного процесса удалось отразить в виде двух отношений третьей степени (3-арных), а сами отношения изобразить в виде таблиц с тремя колонками.
Удобство использования табличной формы для задания отношения определяется в данном случае следующими факторами:
Все используемые множества конечны.
При добавлении или удалении студентов, предметов, преподавателей просто добавляются или удаляются соответствующие строки в таблице.
Нас сейчас не интересует вопрос, хороши ли полученные отношения. Заметим пока только, что, как показывают следующие замечания, не любую строку можно добавить в таблицу "Посещать лекции".
Замечание. В таблицу "Посещать лекции" нельзя добавить две одинаковые строки, т.к. таблица изображает отношение  синтаксического ограничения - такое ограничение задано в определении понятия отношение (одинаковых строк не может быть ни в одной таблице, задающей отношение).
Замечание. В таблицу "Посещать лекции" нельзя добавить кортеж (Иванов, Геометрия, Пушников). Действительно, из таблицы "Читает лекции по…", представляющей отношение
синтаксического ограничения - такое ограничение задано в определении понятия отношение (одинаковых строк не может быть ни в одной таблице, задающей отношение).
Замечание. В таблицу "Посещать лекции" нельзя добавить кортеж (Иванов, Геометрия, Пушников). Действительно, из таблицы "Читает лекции по…", представляющей отношение  семантического ограничения - такое ограничение является следствием нашей трактовки данных, хранящихся в отношении (следствием понимания смысла данных).
семантического ограничения - такое ограничение является следствием нашей трактовки данных, хранящихся в отношении (следствием понимания смысла данных).
Отношение RТранзитивное замыкание
Таблица 5
| Где используется | |
| Болт | Двигатель |
| Болт | Колесо |
| Гайка | Двигатель |
| Гайка | Колесо |
| Двигатель | Автомобиль |
| Колесо | Автомобиль |
| Ось | Колесо |
Таблица 5 Отношение RТранзитивное замыкание 
Транзитивное замыкание отношения
Таблица 6
| Болт | Двигатель |
| Болт | Колесо |
| Гайка | Двигатель |
| Гайка | Колесо |
| Двигатель | Автомобиль |
| Колесо | Автомобиль |
| Ось | Колесо |
| Болт | Автомобиль |
| Гайка | Автомобиль |
| Ось | Автомобиль |
Таблица 6 Транзитивное замыкание отношения R
Очевидный смысл замыкания 
Транзитивное замыкание отношений
Транзитивное замыкание отношений
Введем понятие транзитивного замыкания, связанное с бинарными отношениями, которое понадобится в дальнейшем.
это неопределяемое понятие, представляющее некоторую
Выводы
Множество- это неопределяемое понятие, представляющее некоторую совокупность данных. Элементы множества можно отличать друг от друга, а также определять, принадлежит ли данный элемент данному множеству. Над множествами можно выполнять операции объединения, пересечения, разности и дополнения. Новые множества можно строить при помощи понятия декартового произведения (конечно, есть и другие способы, но они нас в данный момент не интересуют). Декартово произведение нескольких множеств - это множество кортежей, построенный из элементов этих множеств. Отношение- это подмножество декартового произведения множеств. Отношения состоят из однотипных кортежей. Каждое отношение имеет предикат отношения и каждый n-местный предикат задает n-арное отношение. Отношение является математическим аналогом понятия "таблица". Отношения обладают степенью и мощностью. Степень отношения - это количество элементов в каждом кортеже отношения (аналог количества столбцов в таблице). Мощность отношения - это мощность множества кортежей отношения (аналог количества строк в таблице). В математике чаще всего используют бинарные отношения (отношения степени 2). В теории баз данных основными являются отношения степени

